2 Day 2 (January 22)

2.1 Announcements

  • Correction about Canvas

    • Journals should be uploaded to Canvas 24 hours after lecture ends
    • Activity 1 will eventually be uploaded to Canvas (but no due date yet)

  • Please start activity 1

  • Questions/clarifications from journals

    • “What data set can I use for the class project?”
    • “My question is how to deal with uncertainty or any unexpected situation that happens.”
    • “I definitely need to confess that I don’t have a solid understanding of Bayesian statistics.”
    • “The brief mention of telemetry data made me wonder whether we’ll need to deal with very large, irregularly sampled, or noisy time-series data right away, or if we’ll build up to that gradually.”
    • “Difference between dynamic and descriptive approaches”

2.2 Opening example: Human movement

  • The goal of this activity is to show you how cool spatio-temporal statistics is!
  • Human movement modeling with the linear regression model and other fancy tools!
  • Trajectories are a time series of the spatial location of an object (or animal).
    • We can usually pick the object and the time that we obtain its spatial location (i.e., time is fixed)
    • The location is a random variable in most cases, but time can also be a random variable.
  • In-class marathon example (Download R script here)

2.3 Statistical models

  • Read pgs. 77 - 106 in Wikle et al. (2019)

  • What is a model?

    • Simplification of something that is real designed to serve a purpose

  • What is a statistical model?

    • Simplification of a real data generating mechanism
    • Constructed from deterministic mathematical equations and probability density / mass functions
    • Capable of generating data
    • Generative vs. non-generative models

  • What is the purpose of a statistical model

    • See section 1.2 on pg. 7 and pg. 77 of Wikle et al. (2019)
    • Capable of making predictions, forecasts, and hindcasts
    • Enables statistical inference about observable and unobservable quantities
    • Reliability quantify and communicate uncertainty
      • Example using simple linear regression

2.4 Matrix review

  • Column vectors
    • \(\mathbf{y}\equiv(y_{1},y_{2},\ldots,y_{n})^{'}\)
    • \(\mathbf{x}\equiv(x_{1},x_{2},\ldots,x_{n})^{'}\)
    • \(\boldsymbol{\beta}\equiv(\beta_{1},\beta_{2},\ldots,\beta_{p})^{'}\)
    • \(\boldsymbol{1}\equiv(1,1,\ldots,1)^{'}\)
    • In R
    y <- matrix(c(1,2,3),nrow=3,ncol=1)
y
    ##      [,1]
## [1,]    1
## [2,]    2
## [3,]    3
  • Matrices
    • \(\mathbf{X}\equiv(\mathbf{x}_{1},\mathbf{x}_{2},\ldots,\mathbf{x}_{p})\)
    • In R
    X <- matrix(c(1,2,3,4,5,6),nrow=3,ncol=2,byrow=FALSE)
X
    ##      [,1] [,2]
## [1,]    1    4
## [2,]    2    5
## [3,]    3    6
  • Vector multiplication
    • \(\mathbf{y}^{'}\mathbf{y}\)
    • \(\mathbf{1}^{'}\mathbf{1}\)
    • \(\mathbf{1}\mathbf{1}^{'}\)
    • In R
    t(y)%*%y    
    ##      [,1]
## [1,]   14
  • Matrix by vector multiplication
    • \(\mathbf{X}^{'}\mathbf{y}\)
    • In R
    t(X)%*%y
    ##      [,1]
## [1,]   14
## [2,]   32
  • Matrix by matrix multiplication
    • \(\mathbf{X}^{'}\mathbf{X}\)
    • In R
    t(X)%*%X
    ##      [,1] [,2]
## [1,]   14   32
## [2,]   32   77
  • Matrix inversion
    • \((\mathbf{X}^{'}\mathbf{X})^{-1}\)
    • In R
    solve(t(X)%*%X)
    ##            [,1]       [,2]
## [1,]  1.4259259 -0.5925926
## [2,] -0.5925926  0.2592593
  • Determinant of a matrix
    • \(|\mathbf{I}|\)
    • In R
    I <- diag(1,3)
I
    ##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]    0    1    0
## [3,]    0    0    1
    det(I)
    ## [1] 1
  • Quadratic form
    • \(\mathbf{y}^{'}\mathbf{S}\mathbf{y}\)
  • Derivative of a quadratic form (Note \(\mathbf{S}\) is a symmetric matrix; e.g., \(\mathbf{X}^{'}\mathbf{X}\))
    • \(\frac{\partial}{\partial\mathbf{y}}\mathbf{y^{'}\mathbf{S}\mathbf{y}}=2\mathbf{S}\mathbf{y}\)
  • Other useful derivatives
    • \(\frac{\partial}{\partial\mathbf{y}}\mathbf{\mathbf{x^{'}}\mathbf{y}}=\mathbf{x}\)
    • \(\frac{\partial}{\partial\mathbf{y}}\mathbf{\mathbf{X^{'}}\mathbf{y}}=\mathbf{X}\)

2.5 Distribution theory review

  • Probability density functions (PDF) and probability mass functions (PMF)

    • Normal distribution (continuous support)
    • Binomial distribution (discrete support)
    • Poisson distribution (discrete support)
    • And many more (see handout)

  • Distributions in R

    • PDF of the normal distribution \[[z|\mu,\sigma^2] = \frac{1}{\sqrt{2\pi\sigma^2}}\textit{e}^{-\frac{1}{2\sigma^2}(z - \mu)^2}\]
      • \(z\) is the random variable
      • \(\mu\) and \(\sigma^2\) are the parameters
    • PDFs & PMFs in R
      • ?dnorm
    • Generate random variables (\(z\)) from a PDF (e.g., \(z_i\sim\text{N}(\mu,\sigma^2)\))
    z <- rnorm(n = 5, mean = 0, sd = 1)
z    
    ## [1] 1.6583210 0.4404361 0.4330551 0.0216365 0.1167306
    • Histogram representation of a PDF
    library(latex2exp)
z <- rnorm(n = 10000, mean = 0, sd = 1)
hist(z,freq=FALSE,col="grey",main = "",
  xlab= TeX('$\\textit{z}$'),
  ylab = TeX('$\\lbrack\\textit{z}|\\mu,\\sigma^2\\rbrack$'))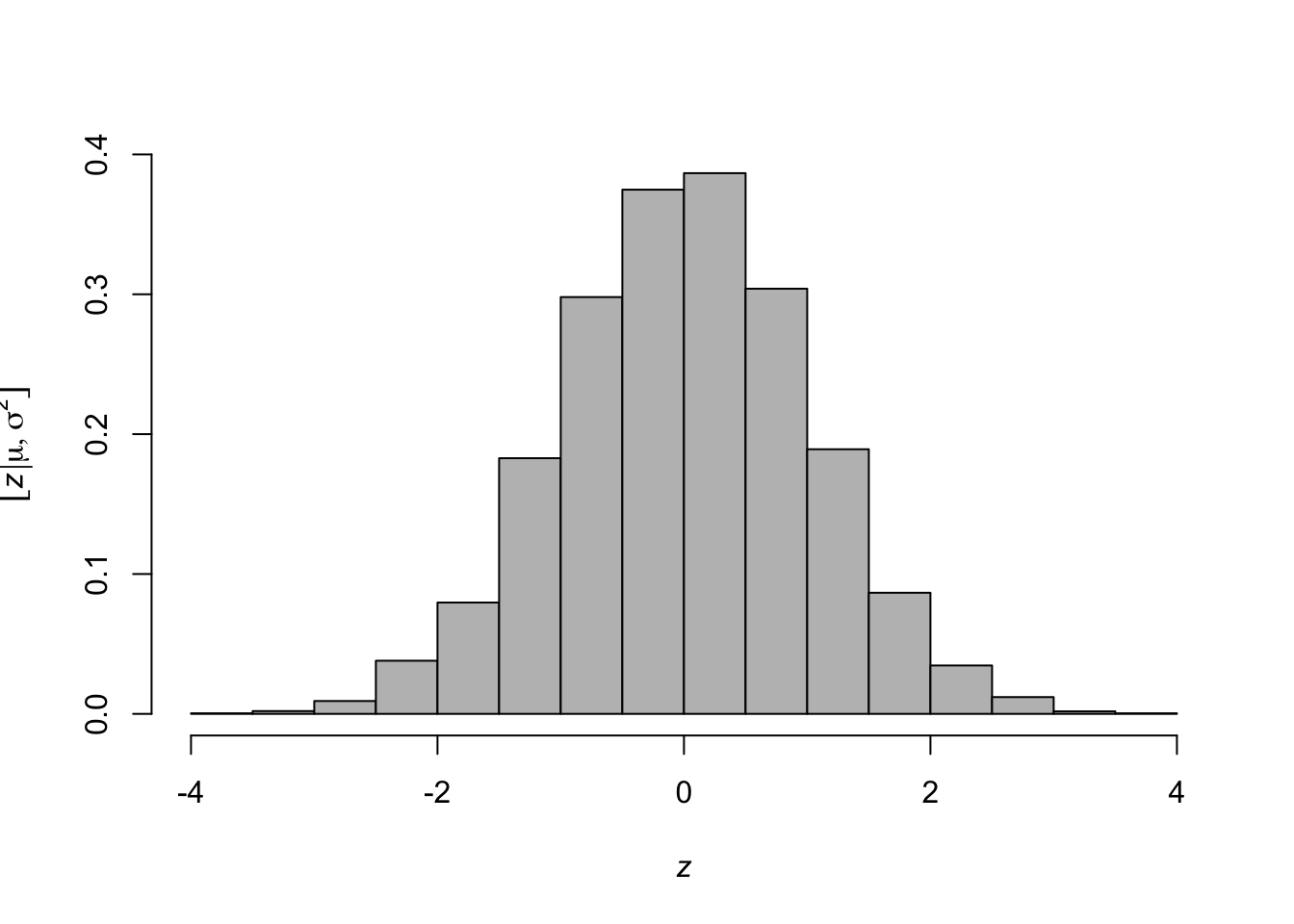

    • Plot a PDF in R
    curve(expr = dnorm(x = x, mean = 0, sd = 1), from = -10, to = 10,
  xlab= TeX('$\\textit{z}$'),
  ylab = TeX('$\\lbrack\\textit{z}|\\mu,\\sigma^2\\rbrack$'))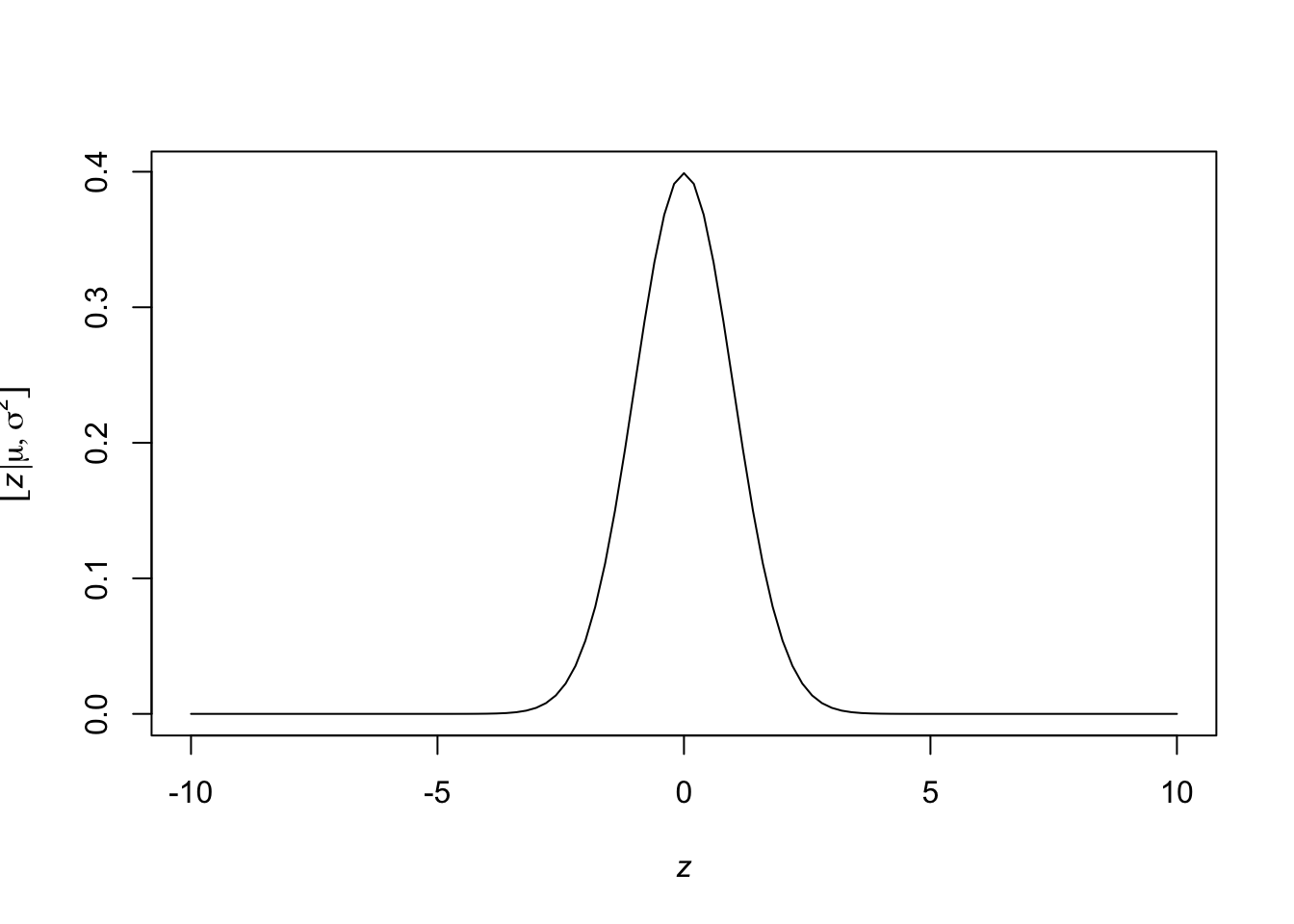

    • Evaluate the “likelihood” at a given value of the parameters
    dnorm(x = 1.759, mean = 0, sd = 1, log = FALSE)
    ## [1] 0.08492566
    • Other distributions
    rpois(n = 5, lambda = 2)
rbinom(n = 5, size = 10, prob = 0.5)    
runif(n = 5,min = 0,max = 3)
rt(n = 5,df = 1)
rcauchy(n = 5, location = 2, scale = 4)
    • See stats package for more information

  • Making your functions for a distribution

    • PDF of the exponential distribution \[[z|\lambda] = \lambda\textit{e}^{-\lambda z}\]
    • Make your own function for the PDF of the exponential distribution
    dexp <- function(z, lambda){lambda*exp(-lambda*z)}
    • Make your own function to simulate random variables from the exponential distribution using the inverse probability integral transform
    rexp <- function(n, lambda){
  u <- runif(n)
  -1/lambda*log(1-u)
}
    • Make histogram by sampling from rexp() and overlay the PDF using dexp()
    z <- rexp(n = 10000, lambda = 1)
hist(z,freq=FALSE,col="grey",main = "",
  xlab= TeX('$\\textit{z}$'),
  ylab = TeX('$\\lbrack\\textit{z}|\\lambda\\rbrack$'))
curve(expr = dexp(z = x,lambda = 1), from = 0, to = 10, 
  add = TRUE,col = "deepskyblue",lwd = 3)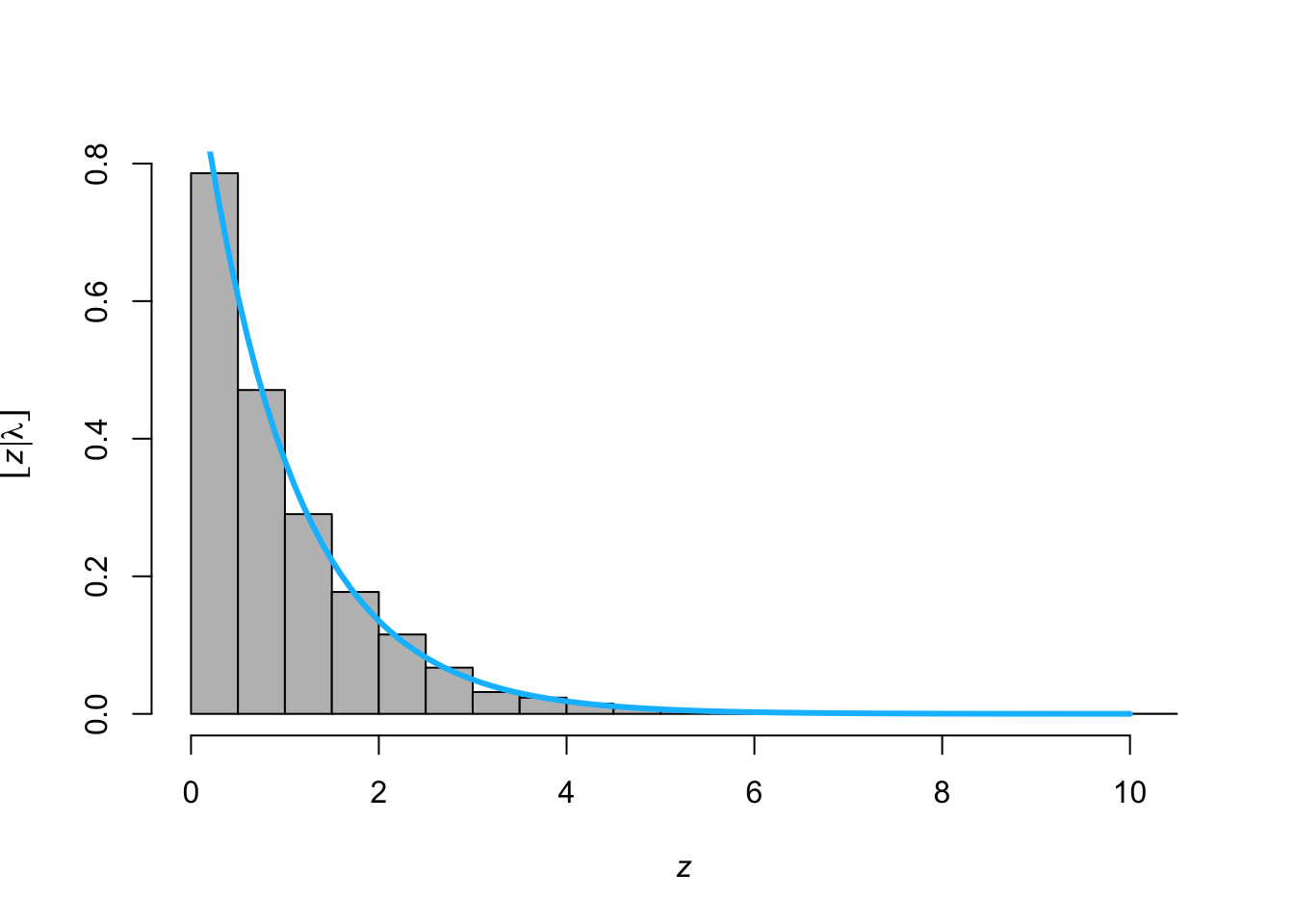

  • Moments of a distribution

    • First moment: \(\text{E}(z) = \int z [z|\theta]dz\)
    • Second central moment: \(\text{Var}(z) = \int (z -\text{E}(z))^2[z|\theta]dz\)
    • Note that \([z|\theta]\) is an arbitrary PDF or PMF with parameters \(\theta\)
    • Example normal distribution \[\begin{eqnarray} \text{E}(z) &=& \int_{-\infty}^\infty z\frac{1}{\sqrt{2\pi\sigma^2}}\textit{e}^{-\frac{1}{2\sigma^2}(z - \mu)^2}dz\\&=& \mu \end{eqnarray}\] \[\begin{eqnarray} \text{Var}(z) &=& \int_{-\infty}^\infty (z-\mu)^2\frac{1}{\sqrt{2\pi\sigma^2}}\textit{e}^{-\frac{1}{2\sigma^2}(z - \mu)^2}dz\\&=& \sigma^2 \end{eqnarray}\]
    • Example exponential distribution\[\begin{eqnarray} \text{E}(z) &=& \int_{0}^\infty z\lambda\textit{e}^{-\lambda z}dz\\&=& \frac{1}{\lambda} \end{eqnarray}\]\[\begin{eqnarray}\text{Var}(z) &=& \int_{0}^\infty (z-\mu)^2\lambda\textit{e}^{-\lambda z}dz\\&=& \frac{1}{\lambda^2} \end{eqnarray}\]